​Building Confidence in Model-Based Systems​

Traditionally, the test phase has served as a checkpoint to progress from one development stage to the next. For instance, a prototype undergoes testing based on design criteria, and upon meeting these criteria, the design advances to the next stage of the design process. However, the test data itself is not carried forward alongside the design. The purpose of the design test is solely to ensure the successful completion of the prototype phase. This pattern repeats across all design stages, from market research and conceptual development to production and maintenance testing. Consequently, as the product is developed, valuable test data is left behind, resulting in the loss of significant learning opportunities.

Adding to this complexity, many companies have shifted from a sequential design methodology to a more flexible and agile approach to product development. The traditional linear and solitary progression of the development process has evolved. As a result, testing is now a continual and ongoing aspect that permeates every stage of development.

The adoption of agile development and the need to disseminate data and insights has brought focus to a pivotal question—how can information be effectively captured and shared across the complete development process?

The act of storing and transmitting data itself is not inherently difficult. However, effectively managing that data is a challenge that engineering teams have grappled with for a long time. How can one guarantee that the data reflects the most up-to-date information? Addressing this question forms a fundamental principle in digital engineering—establishing a singular, authoritative source of truth. Without a disciplined approach to data management, including the establishment of a single source of truth, teams cannot use the information with a sense of certainty and confidence.

Throughout the development cycle, the authoritative source of truth should evolve accordingly. With each round of testing, new information acquired should be integrated into the existing body of knowledge. Rather than considering testing as a series of discrete steps within the development process, it should be viewed as a means to establish a robust knowledge foundation that enhances product development.

Viewing test as a series of steps is key to making the test process efficient. This approach relies on an engineering team’s ability to address two critical questions:

“How will we preserve and carry forward information learned in previous phases? What new information do we need to learn with each new test phase?”

The sum of this information can be referred to as the digital thread, which carries information through the development process. The digital thread becomes the single authoritative source of truth and includes digital artifacts such as a requirements list, digital models, sensor mapping, recorded test data, modeled behavior, performance variations, as-manufactured defects, individual variations, and real-world use history. The digital thread answers the first question of how to capture and retain information through the development process. Improving the quality of the digital thread becomes the primary challenge to a team tasked with implementing a digital engineering process.

The second question, which pertains to capturing necessary information during each new test, can help enhance efficiency within the development process. The accuracy and completeness of the response to this question will determine the quality of the digital thread upon completion.

There are at least two major factors that contribute to errors in a system comprised of modules. Errors arise from the interactions between modules and also result from how these interactions modify the behavior of individual components. Modeling these effects may prove considerably more challenging than modeling the behavior of individual components. These considerations should guide decisions in test engineering during later stages of development. The objective of testing must shift from simply qualifying for the next phase to establishing trust in the digital thread, particularly in the model used to represent the system.

Different models accomplish different goals. Models can be used to visually represent a concept, prioritizing feedback collection for guiding product design rather than focusing on precise functionality. Models can be employed to track requirements or compile a bill of materials for purchasing purposes. Models can also act as physical placeholders within a system until the actual component becomes available, where functionality may not be crucial. Digital models may find utility in scenario testing like finite element analysis or security testing, where the behavior and response of the model become critical. Finally, models can be utilized as digital twins, linked to specific serial numbers and incorporating as-manufactured data that ages over time to mimic the actual usage conditions of the physical system.

Across this range of applications, the demand for accuracy to match the physical system varies. While a conceptual model cannot replicate the exact performance of the physical system, a digital twin used for maintenance prediction requires accuracy that closely aligns with real-world usage and failures. The level of trust placed in the accuracy of a model serves as a gauge for the model’s credibility within the system. Credibility, in this context, refers to “the degree to which individuals are willing to base their decisions on the information derived from the model.”¹

To increase model credibility, we need a way to quantify that credibility and measure progress. The construct proposed by Eann Patterson has been applied to models in multiple fields including material science and is helpful to the current discussion. In this model, Dr. Patterson proposes that models be characterized along two axes: How testable is the model, and how well do we understand the science of the model?

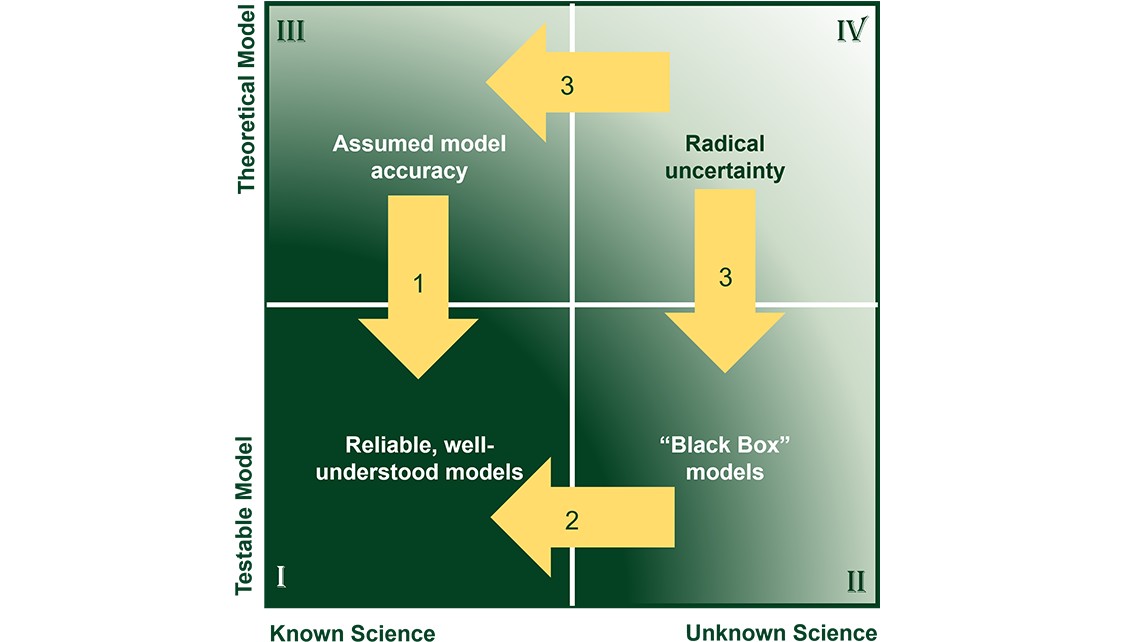
In this framework, the confidence in the model rises as the model is characterized further to the lower left of the graph. It is helpful to segment the field into four segments, as shown in Figure 1, although we must recognize that these lines are fuzzy and not distinct boundaries.

Figure 1. Four Model Categories

In these four segments, we see four categories of models. It is essential to the credibility of a model that engineers understand where the model falls. A brief description of these categories follows:

    I.            Known science with verifiable models—In this box, engineers use a range of tools and metrics to ensure proper application of the models. Examples in this category include mechanical levers, material samples, and ideal physics problems.

    II.            Simplified models that match experimental results well—In this box, the science may not be well understood, but enough data exists that the phenomenon can be accurately modeled. Engineers should use these models with caution, comparing against empirical data. An example of this may be dark matter—we don’t understand the science, but our model of the universe is accurate enough that we can guide space missions.

    III.            Models which have a solid scientific basis but cannot be verified—These models are based on epistemic values to make them viable for use in real-world applications, even when we cannot run tests to verify the accuracy. Examples in this category may include components subject to extreme thermoacoustic fatigue.

    IV.            Models that are difficult to build, difficult to test—A model in this area may be loosely based on known science, but without access to the underlying scientific information or a path to test. The interactions in a black hole may fit into this category.

This construct is helpful to determine how much a model can be trusted. In the next section, we’ll discuss how this helps an engineering team increase their confidence in a given model.

Now that we have identified these categories, we can contemplate strategies to drive models further to the lower left, where confidence increases.

Figure 2. Strategies to Increase Confidence in Models

Shown in Figure 2, the first strategy is to develop better test techniques and technologies. Measurement systems improve every year with better accuracy, precision, speed, and analysis technologies. Every advance in these technologies shifts models from the top left (quadrant III) to the bottom left (quadrant I). As a measurement company, NI is focused on this strategy—making measurements accessible that were previously not.

When faced with a low-confidence model in the upper left, an engineering team can focus their efforts on how to take measurements previously not available. Industry partnerships with measurement companies like NI around specific model problems can yield measurement approaches focused on the most relevant problems.

The second strategy is to drive new scientific understanding into models. The goal of this approach is to develop science-based models to replace black boxes. In this area, NI partners with companies like Ansys to develop physics simulations based on published scientific principles, which are then validated with experimental data. These detailed models are then used to generate reduced order models (ROMs) that can be used to simulate systems, improve instrumentation through sensor optimization, augment physical measurements with virtual sensors, and analyzing failure probability. The combination of physics models with experimental data can be used to quantify uncertainties in the system and build hybrid models which use constitutive laws and machine learning principles to capture residual physics that is often not modeled and perform stochastic analysis to identify most likely failure points in the system.

The third strategy applies to parts of the system that cannot be accurately tested and where the scientific principles are not understood (quadrant IV). Systems here require new research approaches to find ways to measure the phenomena, or to understand the underlying physics. NI partners with academic research programs globally to improve the ability to understand and measure these concepts.

As models become increasingly important, engineers must find ways to trust them for use as part of the test plan. An important part of relying on models is understanding where they can be trusted and where further data is required to correctly understand the behavior of the test article. Working with tools from NI, you can collect data at every step of the design process to improve the accuracy of your models. Then, before making assumptions based on those models, you can use NI data acquisition and analysis tools to validate that your model behaves the way you predicted. All of this results in a higher level of confidence in your model so that you can leverage the power of digital engineering tools.

• Learn more about NI's complete portfolio of data acquisition products